In regular algebra, we can combine simple operations into more complex statements; for example, we can write an expression which includes both addition and multiplication: 4x+7, because we have rules which tell us that when we encounter this expression, we always do the multiplication first, and then the addition.
Now that we have learned about four operations on sets: union, intersection, difference, and complement, we want to be able to write more complex expressions, such as (A∪B′)∩A, for example. We want to be able to draw venn diagrams of these compound expressions, and we want to be able to calculate the result for these compound expressions if we are given the exact contents of each of the sets involved.
Before we go any further in our exploration of compound operations on sets, we need to be sure we understand some important points about how to draw a Venn diagram.
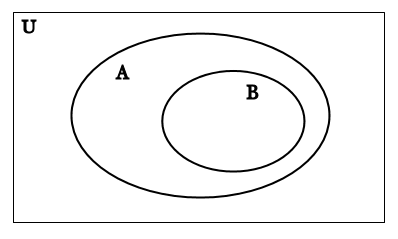
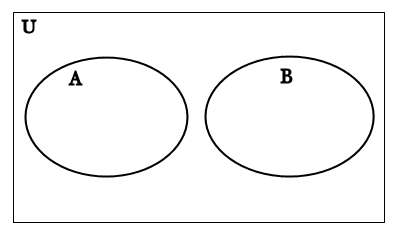
When drawing Venn diagrams, we must be careful not to make assumptions about relationships between sets when we don’t know anything about the sets themselves. If we have two sets there are 3 possible ways they could be related:
Let’s call our two sets A and B.
One set is a subset of the other: (Here B is a subset of A.)
The two sets are disjoint:
The two sets intersect:
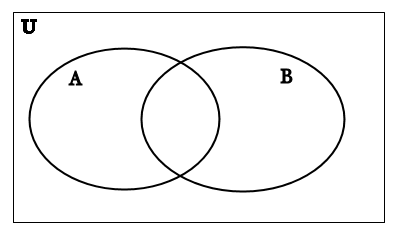
When we don’t know anything about the sets we are working with, we always draw them as though they overlap:

Why does this work? We'll shade some areas different colors for a moment to help us explain why. In this next diagram, we have shaded the set A in red and the set B in blue; purple indicates where both red and blue have been shaded.
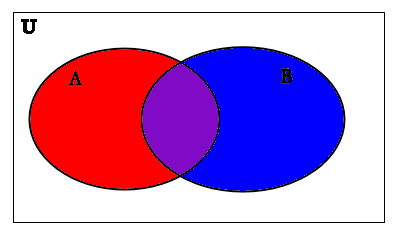
If the two sets are DISJOINT, this picture still works if we assume that A∩B is EMPTY. Remember that A∩B is purple region in the middle where A and B overlap.
If A⊆B, then this picture still works if we assume that A-B is EMPTY. Remember that A-B is just the red area of A to the left (it does not include the purple area of A where it intersects with B.
If B⊆A, then this picture still works if we assume that B-A is EMPTY. Remember that B-A is just the blue area of B to the right (it does not include the purple are of B where it intersects with A.
If you are drawing a Venn diagram in order to solve a problem and you have no idea what the two sets are, be sure to draw your diagram like this so that the two sets overlap.
It is important to understand that we can never assume that an arbitrary set is not empty.
Just because a set takes up space on a Venn diagram doesn’t mean it necessarily has any elements. For example, if A were actually an empty set in the venn diagram above, then this would mean that the red shaded area and the purple shaded area (where there is also red shading) will both be empty. This means that even though these shaded areas on the diagram take up space, there may be nothing in them.
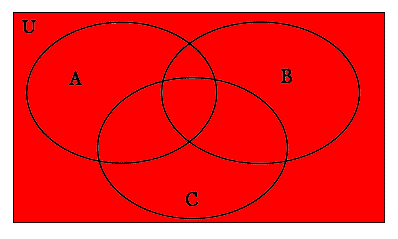
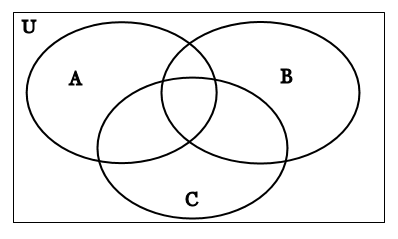
In all of the examples we will be looking at in this section, we will often be working with 3 or more sets. We can draw a Venn diagram with as many sets in it as we like. A general Venn diagram for three sets would look something like this:
It is important to always label your venn diagrams. Whenever you use a venn diagram to represent a set, you should put the label which indicates what the shading depicts above or below the venn diagram. See some of the examples below:
Sometimes we want to combine more than two sets and more than one operation to create a more compound expression. But in order to do this we have to establish some set of rules so that we know in what order to do each operation. Just like with numbers, we use parentheses if we want an operation to be done first.
Just like with numbers, we always do anything in parentheses first. If there is more than one set of parentheses, we work from the inside out.
We do complements first.
Union , intersection, and difference operations are all equal in the order. So if we have more than one of these at a time, we have to use parentheses to indicate which of these operations should be done first. For example, the expression A∪B-C doesn’t make any sense because we don’t know which operation we should do first: should we take the union first, and then the difference, or should we take the difference first and then the union? In order to make this clear, we need to either write (A∪B)-C or A∪(B-C).
Let’s look at some examples. For each of these examples, let U={1,2,3,4,5,6,7,8,9}, A={1,2,3,4,5}, B={2,4,6,8}, C={4,5,6}:
So our Venn diagram will look like this: (I have put each of the elements in its place on the Venn diagram.)
(A∪B)-C
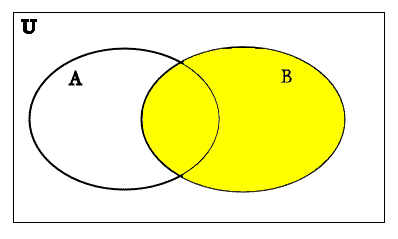
First we find A∪B. In this case, A∪B={1,2,3,4,5,6,8}. On a Venn diagram for A∪B, we would get:
A∪B
Remember that when we take A∪B we ignore the set C. Don’t let the fact that the set C is there distract you. It doesn’t have anything to do with the operation A∪B, so we ignore it for the moment; we’ll use it in the next step.
Next we find (A∪B)-C. Because A∪B={1,2,3,4,5,6,8} and C={4,5,6}, we just substitute these sets in for A∪B and C respectively to get:
(A∪B)-C={1,2,3,4,5,6,8}-{4,5,6}={1,2,3,8}
To create a Venn diagram for (A∪B)-C, we must first have a venn diagram for A∪B and for C, so here is a venn diagram of C, where the set C is shaded in blue:
C
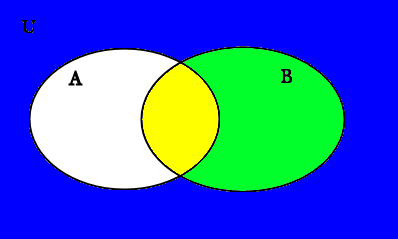
Now we put both these shadings for A∪B and C together on the same venn diagram, and we get the following picture; the set C is in blue, the set A∪B is in red, and the area where they overlap becomes purple:
A∪B in red, C in blue
Now to take (A∪B)-C we simply take away anything that has been shaded blue (this includes the purple part) because we want to keep everything that is in the set A∪B but get rid of anything that is in C. What’s left over is this, which is the Venn diagram of (A∪B)-C:
A∪B
Notice that exactly what is left over in the red shaded region is the set {1,2,3,8}, which is exactly what we got above when we calculated this using only the sets without the diagrams!
A∪(B∩C′)
First we find C′, because we first do what is inside the parentheses; within the parentheses, we have two operations: intersection and complement, and the order of operations tell us to do complement first.
In this case, C={4,5,6}. So C′={4,5,6}′={1,2,3,7,8,9}.
To find a Venn diagram for C′, we would first draw a Venn Diagram for C: (Here C is shaded in blue.)
C
Now to find C′, we shade in any part that was white on the diagram for C, to get the following diagram of C′, where C′ is shaded in red:
C′
Now that we have C′, next we want to find B∩C′. Because B={2,4,6,8} and C′={1,2,3,7,8,9}, by substituting these sets into B∩C′ we get:
B∩C′={2,4,6,8}∩{1,2,3,7,8,9}={2,8}
To make a Venn diagram of B∩C′, we first need a venn diagram of B and a venn diagram of C′. In our venn diagram of B, we shade B in blue:
B
Now we put our venn diagrams for B and for C′ together; we shade in C′ in red and B in blue so that the area where B and C′ overlap is purple. Notice that this purple area is where C′ and B intersect, and so the numbers in the shaded purple are exactly the elements of the set {2,8}!
C′ in red, B in blue
So we take only the purple region where B and C′ intersect and draw our Venn diagram of B∩C′ like this:
B∩C′
Now we can take A∪(B∩C′). Because we now know that B∩C′={2,8}, and A={1,2,3,4,5}, we can substitute these sets into A∪(B∩C′) to get:
A∪(B∩C′)={1,2,3,4,5}∪{2,8}={1,2,3,4,5,8}.
Be careful! Remember that when we take the UNION, we put ALL the elements of both sets together. This is the OPPOSITE of taking the INTERSECTION, where we only take the elements that are in BOTH sets at the same time! Be careful not to confuse the union with the intersection.
To get a Venn diagram for A∪(B∩C′), we need to have venn diagrams for A and for B∩C′. We draw a venn diagram of A by shading A in yellow:
A
So now we put our shading for A together with our shading for B∩C′ so that A is shaded yellow and B∩C′ is shaded purple on the same venn diagram. Where the yellow set A and the purple set (B∩C′) overlap, we end up with a kind of blue-green, so that the picture looks like this:
A in yellow, B∩C′ in purple
Because we want to take the UNION of the yellow set A and the purple set B∩C′, we take the whole shaded area, where there is yellow and where there is purple and where the yellow and purple overlap to make blue-green. To make our final Venn diagram clear, we shade the whole area in a single color (here we pick orange):
A∪(B∩C′)
Notice that our final shaded area is the set {1,2,3,4,5,8}, which is exactly the answer we got for A∪(B∩C′) above!
For any given sets and operations, we can do the operations either by drawing several Venn diagrams step-by-step, or we can simply work with the elements in the sets themselves. Pay attention to instructions to decide which of these methods a question is asking you to use.
Typically, if we know what the sets are, we will just calculate the answer, but if we don't know what the sets are, we will draw venn diagrams, because venn diagrams are the only way that we can represent abstract sets that we don't know anything about!
We can also use Venn diagrams to prove that two expressions are equal. If we want to show that two expressions involving sets and set operations are actually equal no matter what the sets are, all we need to do is to draw a venn diagram of each expression and show that the two venn diagrams are identical.
For example, when we learned the definitions of complement and difference, we realized that A′ and U-A are the same. So we can write A′=U-A. The best way to prove that two expressions are the same is to draw their Venn diagrams and show that they have exactly the same area shaded.
We know that A′ has the following Venn Diagram:
A′
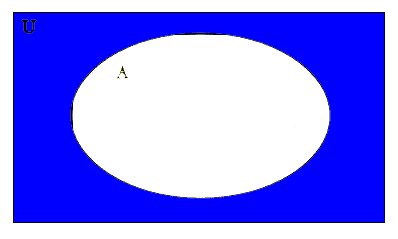
Now let's draw a venn diagram of U-A. First we must have a venn diagram of U and a venn diagram of A.
U
Here the set U is shaded in red. Notice that this is the whole venn diagram, because the universal set always includes everything.
A
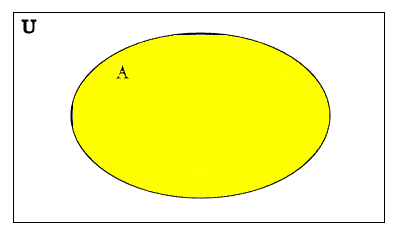
Here the set A is shaded in yellow.
Now we put both U and A together on the same venn diagram, so that A is shaded yellow and U is shaded red, so that the places where the red and the yellow overlap are orange:
A is yellow, U is red
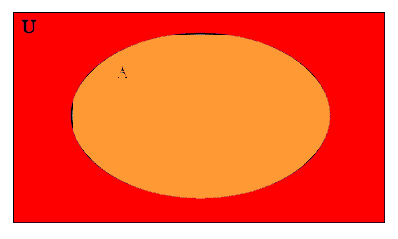
To take the difference U-A, we must begin with U, the red shaded part, and remove any parts which were in A, or which were shaded yellow. Since the orange portion of this diagram was shaded yellow, we must remove that from the diagram to get the diagram for U-A:
U-A
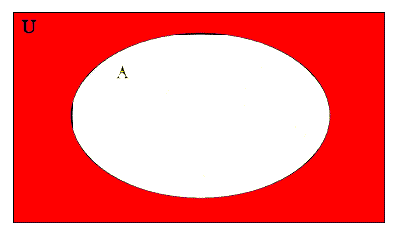
Notice that the venn diagram for A′ and the venn diagram for U-A are identical! This proves that A′=U=A, no matter what the sets U and A contain!
Be careful - You CANNOT prove that two expressions are always equal by giving EXAMPLES of specific sets that would make the expressions equal; you can only do this by showing that their venn diagrams are equal. This is a very important concept in mathematics: AN EXAMPLE IS NOT A PROOF! Make sure you know the difference between an example and a proof!
To illustrate this idea, let’s come up with both an example and a proof for a few different problems:
A-B=(A′∪B)′
First let’s come up with an example. If we make A={15,20,25} and B={20,30}, and U={5,10,15,20,25,30}, then:
A-B={15,20,25}-{20,30}={15,25}
To find (A′∪B)′, we need to find A′ first, because it is inside the parentheses, and complements come first. Here A′={5,10,30}.
Next we can find A′∪B={5,10,30}∪{20,30}={5,10,20,30}.
Then we can find (A′∪B)′={5,10,20,30}′={15,25}.
Because A-B={15,25} and (A′∪B)′={15,25} we can say that A-B=(A′∪B)′.
But this is just an EXAMPLE! This only shows that A-B=(A′∪B)′ when A={15,20,25} and B={20,30}, and U={5,10,15,20,25,30}.
We cannot tell if A-B=(A′∪B)′ is true for ALL POSSIBLE SETS A and B! So this is NOT a proof!
Now let’s try a proof. The only way to prove that A-B=(A′∪B)′ for all possible sets A and B is to show that the Venn diagram of A-B is the same as the Venn diagram for (A′∪B)′.
First we recall that the Venn diagram of A-B looks like this:
A-B
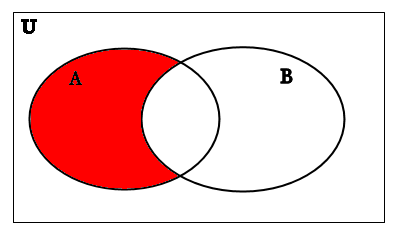
Now we need to construct the Venn diagram for (A′∪B)′ step by step to show that it is exactly like the one above.
To do this we must first draw A′, (which we already did in a previous example, so we'll just use that diagram here) because we must do what is in the parentheses first, and the complement comes before every other operation.
The Venn diagram of A′ is:
A′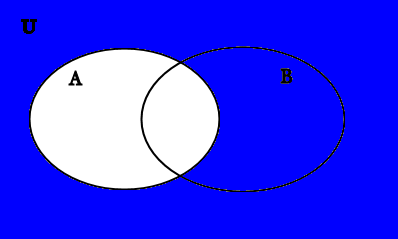
Now we take the venn diagram of B:
B
Be careful - Notice here that we have an oval indicating the set B in the Venn diagram for A′ and we have an oval indicating the set A in the Venn diagram of B, which is not necessary in general. HOWEVER, since in this case, we need these Venn diagrams only as a step to create the Venn diagram of (A′∪B)′, and THIS FINAL EXPRESSION contains BOTH sets A and B, then BOTH an oval indicating the set A AND an oval indicating the set B must be in EVERY Venn diagram which we make leading up to our Venn diagram for (A′∪B)′. If the Venn diagram for A′ were missing an oval indicating the set B or the Venn diagram for B were missing an oval indicating the set A, then we wouldn't be able to put them together on the same Venn diagram to take the union.
Now we shade in B in yellow and A′ in blue on the same venn diagram so that we can find A′∪B. The areas on the Venn diagram where the yellow B and the blue A’ overlap become green:
A′ in blue, B in yellow
We want to take the union of the yellow set B and the blue set A′, so we take everything that has been shaded yellow or blue (or green where both yellow and blue overlap). To make our diagram clearer, we recopy it so that it is all in one color, so the Venn diagram we get for A′∪B is:
A′∪B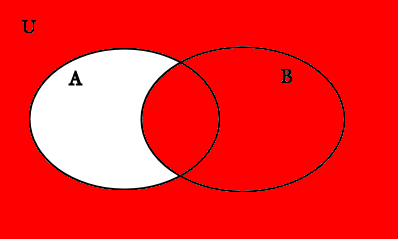
Now we need to find (A′∪B)′ . So we want to take the complement of the red shaded area above which represents the set A′∪B. We recall that a complement is everything that is in the universal set but not in A′∪B. The area that is in U but not in A′∪B is exactly the white area on the Venn diagram. So to shade in (A′∪B)′ , all we need to do is shade in the area that was white in the above venn diagram like this:
(A′∪B)′ 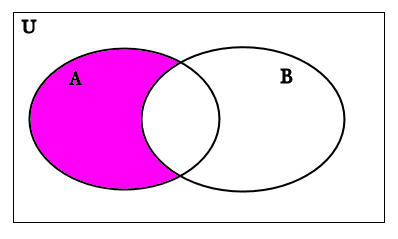
This is the same as the Venn diagram for A-B! So we have PROVED that A-B=(A′∪B)′!
This is a proof because the Venn diagrams are all general and don’t require us to know what A and B are.
We have shown, by using the Venn diagrams, that A-B=(A′∪B)′ for ALL sets A, B and U. A, B, and U can be ANYTHING, and A-B=(A′∪B)′ will still be true!
If we want to prove that two sets are NOT equal, all we have to do is show that their Venn diagrams are not the same:
Let’s consider A∪B=A∩B. Is this always true? Sometimes true? Or never true?
To see if it is true in the general case, let’s draw the Venn diagrams:
We recall from previous examples that A∪B has the Venn diagram:
A∪B
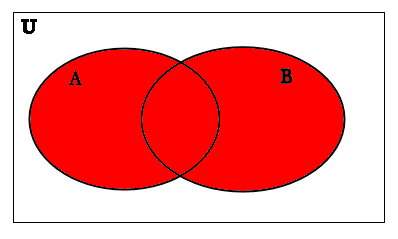
We also recall from previous examples that A∩B has the Venn diagram:
A∩B
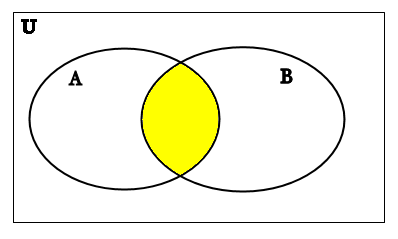
These two diagrams are NOT the same! This means that it is NOT true that A∪B=A∩B for ALL POSSIBLE SETS A and B.
However, there might be some sets for which A∪B=A∩B.
Clearly if A={1,2,3} and B={2,4,6}, A∪B={1,2,3,4,6} and A∩B={2}. Obviously {1,2,3,4,6}≠{2}.
But if A={1,2,3} and B={1,2,3}, then A∪B={1,2,3} and A∩B={1,2,3} so in this case A∪B=A∩B.
So A∪B=A∩B is true SOMETIMES but NOT ALWAYS.
If you look carefully, you’ll notice that A∪B=A∩B will be true only when A=B. To see this, look at the Venn diagrams above. The only way to make the red shaded area and the yellow shaded area the same would be to squish the sets A and B together into one set so that they are exactly the same set.
Right now we will do another example showing how we can prove that two compound expressions containing sets are equivalent. This example is actually one of two well-know rules in set theory, called DeMorgan's Laws (after the mathematician who discovered them).
Once set theory was invented, and we have compound expressions involving sets and multiple operations, it becomes natural to ask if two different compound expressions are actually equal. For example, with regular algebra using numbers and operations on numbers such as addition, subtraction, multiplication, and division, there are rules that say that you can rewrite 3(4x+2) as 12x+6 by distributing the multiplication over the addition. Is the same process true for sets?
For example, can I write (A∪B)′ as A′∪B′? In other words, can I distribute set complement over set union? The only way to tell is to draw a Venn diagram of (A∪B)′ and a Venn diagram of A′∪B′ and see if the two Venn diagrams are identical:
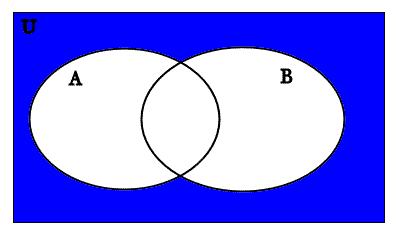
We begin by drawing the Venn diagram of (A∪B)′:
We recall from a previous problem that the Venn diagram for A∪B looks like this: (remember that because the union is inside the parentheses, we must do it before we take the complement, which is outside the parentheses)
A∪B
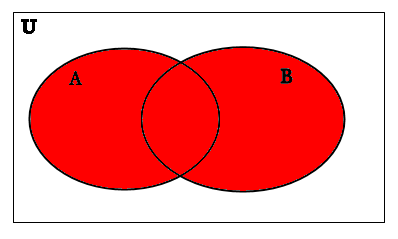
(A∪B)′
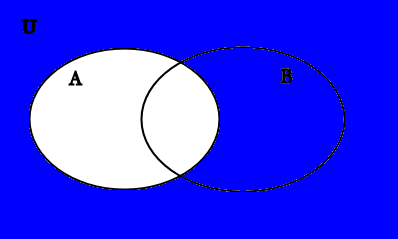
Now we draw the Venn diagram of A′∪B′. We begin with the Venn diagrams for A′ and B′, which we recall from previous examples:
A′
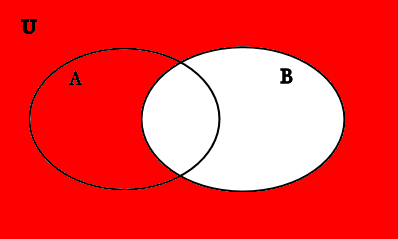
B′
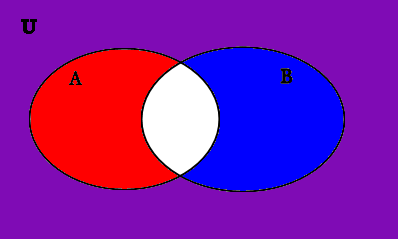
Now we need to put A′ and B′ on the same Venn diagram. Because A′ is in blue and B′ is in red, the area where they overlap will be purple:
A′ in blue, B′ in red
Because we are taking a union, we keep everything that has been shaded in blue or red (or purple, because the purple comes from both red and blue shading). To make our diagram clearer, we choose to shade in all one color, so that this is the diagram of A′∪B′:
A′∪B′
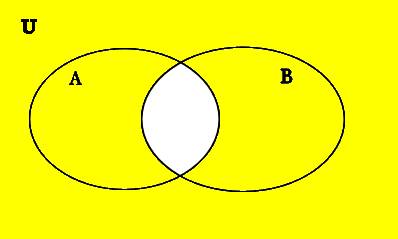
This is clearly not the same as the Venn diagram for (A∪B)′! So we can conclude that in general, (A∪B)′ cannot be replaced with A′∪B′ without changing the resulting set!
Be careful! You can NEVER replace (A∪B)′ with A′∪B′, because these two sets are NOT (in general) equal! If you are asked to draw a Venn diagram for (A∪B)′, for example, be sure to follow the order of operations - NEVER begin by taking the complements of A and B, because that is OUTSIDE the parentheses! Likewise, you CANNOT replace (A∩B)′ with A′∩B′, because these two sets are NOT (in general) equal! (To see this, try drawing a Venn diagram of each side and compare them.)
It turns out that there actually is a kind of twisted distribution rule that allows you to "distribute" set complement over set union (or intersection)
It turns out that the following two rules are ALWAYS true for ANY two sets A and B:
1) A′∪B′=(A∩B)′
2) A′∩B′=(A∪B)′
These rules are called DEMORGAN’S LAWS.
How do we know that these two rules will always be true?
Let's start with the first rule - how do we know that A′∪B′ will always be equal to (A∩B)′, no matter what the sets A and B are? We draw Venn diagrams of each side of this equation, and show that they turn out to be the same.
First we draw a Venn diagram of A′∪B′; since we just did this in the previous example, we can simply use that same diagram here:
A′∪B′

Now let’s construct the Venn diagram for (A∩B)′:
Because we always do what is in the parentheses first, we first draw a Venn diagram of A∩B, which we have from a previous example:
A∩B
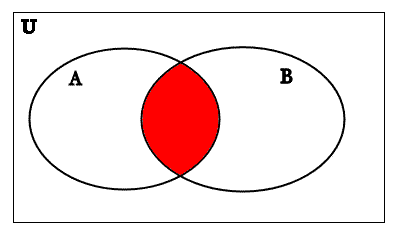
Now we take the complement of by shading in the white area in the diagram above (Remember that the complement is everything that is NOT in A∩B!):
So we get the following Venn diagram for (A∩B)′:
(A∩B)′
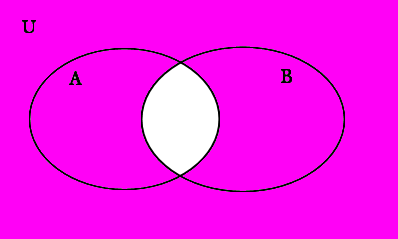
This is the same Venn diagram we got for A′∪B′.
So we have proved DeMorgan’s First Law: A′∪B′=(A∩B)′, because the Venn diagrams of each side of the equation are identical.
Sometimes you may need to draw Venn diagrams of the Null Set Ø or the Universal set U. To draw a Venn diagram of the null set, we need only draw any Venn diagram without any shading. Below are several examples of different Venn diagrams of the null set:
Ø

Ø
Ø 
Ø 
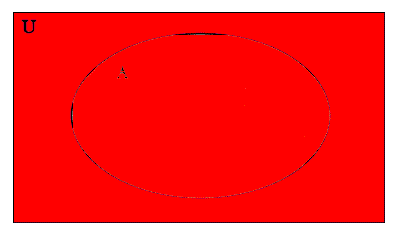
To draw a Venn diagram of the Universal set, we shade in everything. Below are several different examples of Venn diagrams of the universal set:
U

U
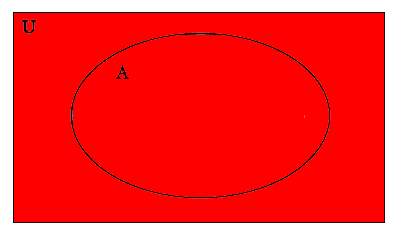
U
U