

So far we have mostly focused our attention on finite sets (that is, sets which are not infinite). But you may have noticed that most of the sets we work with in mathematics: the set of integers, the set of rational numbers, the set of real numbers, etc., are NOT finite! These sets all have an INFINITE number of elements, so they are called INFINITE SETS.
Infinity can be a very tricky concept, but a very interesting one. If you start to think about infinities, you will eventually come up against the question:
“Are all infinities the same size?”
The answer, as it turns out, is “no.” So some infinities are “bigger” than others!
For example, the the set of integers (Remember that the the set of integers includes all positive and negative whole numbers, including zero) goes on forever. If I asked you how many integers there are, you would have to say, “infinitely many.” But the the set of real numbers also goes on forever, and the the set of integers is a PROPER subset of the the set of real numbers. So there must be more real numbers than integers, or in other words, the cardinality of the the set of real numbers must be a "bigger infinity" than the cardinality of the the set of integers, right?
On the other hand, we could argue that adding more elements to an already infinite quantity of elements doesn't change that infinite quantity. Yes, we could say, there are more real numbers than there are integers, but since both the number of real numbers and the number of integers is infinite, the cardinalities of these two sets is the same, because you cannot have one infinite quantity which is bigger than another! In other words, you could argue, adding something or multiplying something by infinity won't change that infinity.
So, which of these arguments is right? Well, they both make important and correct points, but in this case, the cardinality of the set of real numbers is in fact "bigger" than the cardinality of the set of integers, even though they are both infinite quantities. However, the reasons for this are a little more complex than it seems at first.
Let’s try to take a look and see if we can figure out how to tell one kind of infinity from another:
We’ll start by looking at the the set of natural numbers. Clearly the the set of natural numbers has an infinite cardinality because the integers go on forever. (Remember that the word cardinality just refers to the number of elements in the set.) We can get away with calling infinity a number as long as we understand that it is a new, strange kind of “number” that does not follow the rules that regular finite numbers follow. (Technically, we should not call infinite amounts numbers at all, because numbers technically only include finite amounts, but to keep the language of this lecture more readable, we'll keep calling infinite amounts "numbers" with the quotation signs around it. Real mathematicians actually refer to infinite amounts as infinite quantities rather than infinite "numbers.")
We don’t know any infinite “numbers” yet, but we can see that some infinite “number” must exist in order to describe the number of elements in the set of natural numbers. So we decide to just give this infinite “number” a name. We call it ℵ0. We call this symbol ℵ0 “aleph-null.” Aleph is just the first letter in the Hebrew alphabet, and null just refers to the 0 subscript. ℵ0 is not a number in the way that 5 or 12 million or 3.79384509 is a number. We cannot count ℵ0 out on our fingers, or measure it; we need to just become comfortable with the idea that ℵ0 is simply DEFINED to be the cardinality of the natural numbers, which is a certain infinite "number" . Because ℵ0 is infinite, it is very large – so large that we cannot write it down except to write ℵ0.
We have to be careful with infinite “numbers.” They may not behave the same way that regular finite numbers do. For example, if you add 1 to any regular finite number, you get a new number, different from the number you started with. Formally we would write this:
For any finite number n, n+1≠n.
To see that this is true, suppose that n=n+1.
Subtracting n from each side gives us 0=1.
This is clearly false, so our assumption that n=n+1 must be false.
Therefore we can conclude that for any finite number n, n+1≠n.
This turns out NOT to be true with INFINITE "numbers" like ℵ0!
Another important property of finite numbers is that if you multiply any non-zero finite number by 2, you get a new number, different from the number you started with. Formally we would write this:
For any finite non-zero number n, 2n≠n.
To see that this is true, suppose that n=2n.
Dividing both sides by n gives us 1=2.
This is clearly false, so our assumption that n=2n must be false.
Therefore we can conclude that for any finite non-zero number n, 2n≠n.
This also turns out NOT to be true with INFINITE "numbers" like ℵ0!
So how on earth do we decide if two infinities are equal or not? The answer to this question brings us back to infinite sets and their cardinalities.
Here’s how mathematicians have decided to cope with this problem of determining when two infinite cardinal "numbers" are the same size:
If two sets have the same number of elements, then we ought to be able to establish what we call a ONE-TO-ONE CORRESPONDANCE between the two sets. A ONE-TO-ONE CORRESPONDANCE is a process by which we take each element in the first set and pair it with a single, unique element from the second set. Essentially what this means is that we pair up every element in the first set with an element in the second set so that every number in each set is paired with one and only one other number in the other set.
If we can establish a one-to-one correspondence between two sets, then we have proved that the two sets have the same cardinality.
For example:
If we take the sets {1,2,3} and {1/4, 1/3, 1/2}, we can establish a one-to-one correspondence in several different ways. One way would be to set up this one-to-one correspondence:
1 → 1/4
2 → 1/3
3 → 1/2
So the 2 and 1/4 are paired up, 2 and 1/3 are paired up, and 3 and 1/2 are paired up. Each element from the first set is paired up with exactly one element of the second set. No elements in either set were skipped, and no elements from either set were used more than once in the pairing. So the sets {1,2,3} and {1/4, 1/3, 1/2} have the same cardinality. Because these two sets are finite, we can obviously tell that this is true; obviously both sets have cardinality 3.
Notice, however, that the one-to-one correspondence that we've used here is not the only way to set up a one-to-one correspondence between the two sets; there are several other possible one-to-one correspondences. For example, another way would be to set up a one-to-one correspondence between these two sets would be to do this:
1 → 1/3
2 → 1/2
3 → 1/4
For these two sets, there are actually 6 possible ways to set up a one-to-one correspondence between the two sets. We've shown you two possible ways here. Can you find the 4 other possible ways to set up a one-to-one correspondence between these two sets?
If we take the sets {1,2,3} and {2, 3, 4, 5}, we cannot establish a one-to-one correspondence between the two sets. To see this, try to line up each element of the first set with one element of the second set. If we pair one of the elements of the first set with the number 2 in the second set, and then pair up a second element of the first set with the number 3 in the second set, and then pair up a third element of the first set with the number 4 in the second set, there will be no more elements in the first set to pair up with the number 5 in the second set! So we can’t put the sets into one-to-one correspondence and the two sets do not have the same cardinality. This is clear as the first set has cardinality 3 and the second set has cardinality 4, and obviously 3 does not equal 4!
Setting up one-to-one correspondences between two finite sets is not really interesting, because we can always tell whether or not two finite sets have the same cardinality simply by counting how many elements there are in each set. But with infinite sets, we cannot count all the elements in each set, because they go on forever! So, in order to find the cardinality of infinite sets, we must try to put them into one-to-one correspondence with other infinite sets!
With infinite sets, really what we are interested in is this: does a given infinite set have the same cardinality as the set of natural numbers? To answer this questions, we simply try to put a set into one-to-one correspondence with the set of natural numbers; if it is possible to do this, then the infinite set in question has the same cardinality as the set of natural numbers.
Let’s begin by taking a look at the set of whole numbers. So far, the only infinite “number” we know is ℵ0. This describes the cardinality of the set of natural numbers. But clearly the cardinality of the set of whole numbers is infinite, too, because the whole numbers go on forever. The set of natural numbers is a proper subset of the set of whole numbers, because the number 0 is a whole number, but not a natural number. So the cardinality of the set of whole numbers must be bigger than the cardinality of the set of natural numbers, right? Actually, NO! If we can put the two sets into one-to-one correspondence, then their cardinalities are equal, even if one set seems to have “more” elements than the other! We'll come back to this idea later.
For now, let's see if we can set up a one-to-one correspondence between the set of natural numbers and the set of whole numbers:
We can start by writing the natural numbers as N={1,2,3,4,…} and the whole numbers as Z*={0,1,2,3,4,…}.
Now we set up the following correspondence:
1 → 0
2 → 1
3 → 2
4 → 3
.
.
.
Let's check to see if this is really a one-to-one correspondence. Remember that a one-to-one correspondence pairs every element of the first set with one and only one element of the second set and vice versa.
So to show that a pairing is a one-to-one correspondence, we need only show that:
There is a REGULAR PATTERN here that we can continue FOREVER.
If we continue this pattern, we will NEVER RUN OUT OF NUMBERS to pair up from each set, and we will NEVER SKIP any numbers in either set.
Does this pairing satisfy these two criteria?
Is there a regular pattern here? Yes. The pattern is that each natural number is sent to the whole number which is one less than the natural number. Formally, if we let n symbolize the natural number which we are trying to pair up, then n will always be paired with n-1. This is definitely a clear pattern. Can this pattern continue forever? In other words, for an arbitrary natural number, will we even have trouble finding a whole number which is one less than it? No. Clearly for any natural number, the number we get when we subtract 1 will always be a whole number. So we can continue this pattern forever.
If we continue this pattern, will we ever run out of numbers to pair up from each set? No. Since both sets are infinite, we cannot run out of numbers in either set. If we continue this pattern, will we ever skip any numbers in either set? No. Since we've started from the beginning of each set, and the number chosen from each set at any given step in the pairing will be one more than the previous number, we can't possibly skip any numbers in either set using this pattern of pairing.
So we have a one-to-one correspondence!
So the cardinality of the set of whole numbers is ℵ0!
Why? Because the set of natural numbers and the set of whole numbers can be put into one-to-one correspondence with one another. Therefore they have the same cardinality. The cardinality of the set of natural numbers is defined as the infinite quantity ℵ0. Therefore the cardinality of the set of whole numbers must be ℵ0.
(This may take a few moments to sink in. It may help to remember that the key idea here is this: if one set has one more element than another and the two sets are finite, we will eventually run out of numbers to pair up with the elements of the larger set. But when the two sets are infinite, we can never run out of numbers to pair up, so in this case, we can establish a one-to-one correspondence, even when one set clearly has one more element than the other.)
What does this tell us about the nature of infinite "numbers"?
It is interesting to note here that, because the set of whole numbers have exactly one more element (the number zero) than the set of natural numbers, we could say that the cardinality of the set of whole numbers is ℵ0+1, or in other words, n(Z*)=ℵ0+1. But because we have just put the set of natural numbers and the set of whole numbers into one-to-one correspondence, we know that the cardinality of the set of whole numbers is ℵ0, or in other words, n(Z*)=ℵ0. So these two quantitiesmust be equal, and therefore we must have ℵ0+1 = ℵ0!
This seems at first like a contradiction, because we know that for any regular finite number n, we cannot have n+1=n.
However, ℵ0 is not a regular finite number. It is infinite. And since we can see that we must have ℵ0+1 = ℵ0, that ℵ0 does NOT behave like regular finite numbers!
In fact, if think about this even more closely, we may notice that if we have ℵ0+1 = ℵ0, then we can add 1 to both sides of this equation to get ℵ0+2 = ℵ0+1, but since ℵ0+1 = ℵ0, we can substitute ℵ0 for ℵ0+1 on the right side of the equation to get ℵ0+2 = ℵ0. Then since we have ℵ0+2 = ℵ0, then we can add 1 to both sides of this equation to get ℵ0+3 = ℵ0+2, but since ℵ0+2 = ℵ0, we can substitute ℵ0 for ℵ0+2 on the right side of the equation to get ℵ0+3 = ℵ0. Notice that we can continue this pattern forever, so we can see that for any regular finite number n, we have:
ℵ0+n = ℵ0
So, adding any regular finite number to ℵ0 does not change it! (Basically, the idea here is that the infinite "number" ℵ0 is so big, that adding anything else that is not infinite will not be enough to change it. Any finite number will be so "small" compared to ℵ0 that it won't change it.)
Now let’s consider the set of integers and see if we can put the set of integers into a one-to-one correspondence with the set of natural numbers. If we can set up this one-to-one correspondence, then the set of integers will also have cardinality ℵ0.
Clearly the cardinality of the set of integers is infinite because the integers go on forever in both directions. The set of natural numbers and the set of whole numbers are both proper subsets of the integers.
Here we will write the integers as Z = {…-3,-2,-1,0,1,2,3,…} and again we will write the natural numbers as N = {1,2,3,…}.
But the problem we encounter is this:
If we try to set up a one-to-one correspondence the way we did in the last example, we might try something like this:
1 → -3
2 → -2
3 → -1
4 → 0
5 → 1
6 → 2
7 → 3
.
.
.
But we need to check to see if this pairing is a one-to-one correspondence:
Is there a regular pattern here? Yes. The pattern is that each natural number is sent to the integer which is four less than the natural number. Formally, if we let n symbolize the natural number which we are trying to pair up, then n will always be paired with n-4. This is definitely a clear pattern. Can this pattern continue forever? In other words, for an arbitrary natural number, will we even have trouble finding an integer which is four less than it? No. Clearly for any natural number, the number we get when we subtract 4 will always be an integer. So we can continue this pattern forever.
If we continue this pattern, will we ever run out of numbers to pair up from each set? No. Since both sets are infinite, we cannot run out of numbers in either set. If we continue this pattern, will we ever skip any numbers in either set? Yes! Notice that in this pairing, we skip all the integers which are less than -3!
So this pairing is not a one-to-one correspondence!
Be careful - this does NOT mean that NO one-to-one correspondence exists between the set of natural numbers and the set of integers. All it means is that THIS PARTICULAR pairing is NOT a one-to-one correspondence. But there may be ANOTHER way of pairing up the numbers from the two sets which will produce a one-to-one correspondence!
Can we find another way to pair up the set of integers with the set of natural numbers which will give us a one-to-one correspondence? Let's try to look at what went wrong with our last pairing, and see if we can learn from that. In our last attempt to pair up all the elements from these two sets, the pattern we used to choose the integers started with a single integer which was in the middle of the set (-3) and then continued to the right, choosing the next number up from the previous one. The problem with this logic is that it leaves any integers which appear to the left of -3 out of our pairing.
How could we try to correct this?
We could try starting with an integer which is farther to the left, for example. Let's suppose that we begin with -10, pairing 1 in the set of natural numbers with the integer -10. Then we would pair 2 in the set of natural numbers with the integer -9, etc. But there are still going to be integers to the left of -10 in the set of integers which are left out of this pairing! So this won't work! Simply moving the number we start with in the integers will not be enough to solve our problem!
We could try changing the pattern of choosing the integers by beginning from a number at the right side of the set, and moving to the left through the set to set up the pairing - will this create a one-to-one correspondence? For example, what if we try the following pairing:
1 → 3
2 → 2
3 → 1
4 → 0
5 → -1
6 → -2
7 → -3
.
.
.
Does this pairing still skip some of the integers? Yes! This pairing skips all the integers which are bigger than 3! So this pairing will not work as a one-to-one correspondence either!
What is the real problem here?
If we look closely, we can see that the real difficulty we are having when we try to pair up the elements of the set of integers with the elements of the set of natural numbers is that the set of natural numbers is only infinite in one direction (to the right), while the set of integers is infinite to both the left and the right. So we will never be able to set up a one-to-one correspondence by using a pattern which chooses the integers by going only to the right or only to the left.
However, remember that the order of the elements in a set does not matter! So if we can think of a way of rewriting the set of integers so that it looks like it is only infinite in one direction, then we should be able to set up a one-to-one correspondence between these two sets!
For example, we could write Z={0,1,-1,2,-2,3,-3,...}. Clearly {0,1,-1,2,-2,3,-3,...}={...,-3,-2,-1,0,1,2,3,...} because these two sets contain exactly the same elements; the elements have just been rearranged. So we have found a way to reorder the integers so that they look as though they are infinite in only one direction.
Another way to look at this reordering is just to keep the set of integers exactly as they are but to "bounce around" the set in the following way:
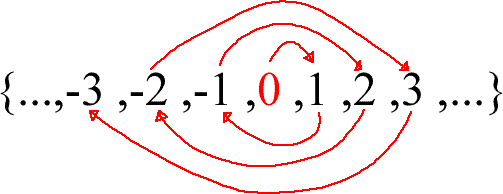
We begin with 0, which is in the middle of the set, then go one to the right, then back to the next number to the left that we have not used, then to the next number to the right that we have not used, then the next number to the left that we have not used, etc.
Now setting up a one-to-one correspondence is easy:
For example, we can now set up the following correspondence:
1 → 0
2 → 1
3 → -1
4 → 2
5 → -2
6 → 3
7 → -3
.
.
.
Let's check to be sure that this is a one-to-one correspondence:
Is there a regular pattern here? Yes. The pattern is that each even natural number is sent to the next integer in the ordering that we have established. Since the ordering involves beginning with 0 and then alternating between the next unused number to the right and the next unused number to the left, this is definitely a clear pattern. Can this pattern continue forever? In other words, for an arbitrary natural number, will we ever have trouble finding an integer to pair with it using the ordering of the integers that we have established here? No. The pattern is that each even natural number is sent to the next integer in the ordering that we have established. Since the ordering of the integers involves beginning with 0 and then alternating between the next unused number to the right and the next unused number to the left, and because the integers go on forever in both of these directions, we can continue this pattern forever.
If we continue this pattern, will we ever run out of numbers to pair up from each set? No. Since both sets are infinite, we cannot run out of numbers in either set. If we continue this pattern, will we ever skip any numbers in either set? No. Since the ordering which we have established in the integers begins in the middle and then alternates between going left and going right, and since we always pick the next unused number in this pattern, we will not leave any integers out of the ordering.
So this pairing is a one-to-one correspondence!
Since we have a one-to-one correspondence between the set of natural numbers and the set of integers, we can conclude that the cardinality of the set of integers is ℵ0!
Be careful - this is NOT the ONLY way to set up a one-to-one correspondence between the set of integers and the set of natural numbers. There are several DIFFERENT ways to set up a one-to-one correspondence here that involve a DIFFERENT ordering of the integers. Can you come up with a DIFFERENT one-to-one correspondence than the one given here? (In fact, there are an INFINITE number of correct ways to set up a one-to-one correspondence between the integers and the natural numbers, each which follows a different pattern!)
What does this tell us about the nature of infinite "numbers"?
It is interesting that ℵ0 describes both the number of natural numbers and the number of integers. This is interesting because the number of integers must be twice the number of natural numbers, because for every positive natural number, there is a positive AND a negative integer. The integers also have 0, which the natural numbers do not. So this tells us that the cardinality of the set of integers must be 2ℵ0+1, or in other words, n(Z)=2ℵ0+1.
But because we can put the set of integers into one-to-one correspondence with the set of natural numbers, we know that the cardinality of the set of integers must be ℵ0, or in other words, n(Z)=ℵ0. So these two quantities must be equal, and this means that 2ℵ0+1 = ℵ0!
This may seem like a contradiction at first, because we know that for any finite number n, 2n+1≠n. But remember that ℵ0 does not behave like a regular finite number, because it is infinite!
Let's look at this more closely: If we have 2ℵ0+1 = ℵ0, and we know from our previous discussion that adding 1 to ℵ0 does not change it, then we can replace ℵ0 with ℵ0+1 on the right to get 2ℵ0+1 = ℵ0+1. Then subtracting 1 from each side gives us: 2ℵ0 = ℵ0.
In fact, if think about this even more closely, we may notice that if we have 2ℵ0 = ℵ0, then we can multiply both sides of this equation by 2 to get 4 ℵ0 = 2ℵ0. But since 2ℵ0 = ℵ0, we can substitute ℵ0 for 2ℵ0 on the right side of the equation to get 4ℵ0 = ℵ0. And since 2ℵ0 ≤ 3ℵ0 ≤ 4ℵ0, and we know that 2ℵ0 and 4ℵ0 both equal ℵ0, we can substitute ℵ0 for both 2ℵ0 and 4ℵ0 in this inequality to get ℵ0 ≤ 3ℵ0 ≤ ℵ0, and therefore we must have 3ℵ0 = ℵ0 also.
Then if we multiply this equation by 2 on both sides, we get 6ℵ0 = 2ℵ0. But since 2ℵ0 = ℵ0, we can substitute ℵ0 for 2ℵ0 on the right side of the equation to get 6ℵ0 = ℵ0. And since 4ℵ0 ≤ 5ℵ0 ≤ 6ℵ0, and we know that 4ℵ0 and 6ℵ0 both equal ℵ0, we can substitute ℵ0 for both 4ℵ0 and 6ℵ0 in this inequality to get ℵ0 ≤ 5ℵ0 ≤ ℵ0, and therefore we must have 5ℵ0 = ℵ0 also.
Notice that we can continue this pattern forever, so we can see that for any regular finite number n, we have:
nℵ0 = ℵ0
So, multiplying ℵ0 by any regular finite number does not change it! (Basically, the idea here is that the infinite "number" ℵ0 is so big, that multiplying it by anything else that is not infinite will not be enough to change it.)
We still have several other infinite sets to look at: the rational numbers, Q, the real numbers, R, and the irrational numbers. Let’s start with the rational numbers. Can we put them into one-to-one correspondence with the natural numbers?
We recall that the set of rational numbers is defined as the set of all numbers which can be written as fractions. Can we put this set into one-to-one correspondence with the natural numbers?
This seems tricky - to simplify this, let's first begin just by writing out all of the positive rational numbers.
If we try two write out all of the positive rational numbers, we'll have to begin like this:

This set is really messy. It doesn't look like the set of natural numbers at all. In fact, this set goes on forever in a bunch of different directions. Every row goes on forever to the right, and every column goes on forever to the bottom. How on earth could we even hope to find a way to put this into a one-to-one correspondence with the natural numbers, since the natural numbers just go on forever in one direction?
From our exploration with the integers, we can see that as long as we can line up the elements of a set in a particular order, we can put the elements into one-to-one correspondence with the natural numbers. This leads us to call infinite sets with the cardinality ℵ0 COUNTABLE because they can always be lined up in a particular order and be “counted.” These sets are infinite, but they can be “counted” if we’re willing to keep counting forever.
So let’s see if there’s any way we can line up the positive rational numbers. Well, if we draw the following diagram, and then go through the rational numbers in the order dictated by the arrows, we can line up all the rational numbers in a particular order:
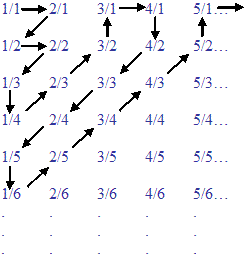
Because the rational numbers go on to the right forever and go on downwards forever, we can just keep going back and forth diagonally to line them all up. So here’s how the correspondence would start:
1 → 0/1
2 → 1/1
3 → 1/2
4 → 1/3 (we don’t sent 4 to 2/2 because 2/2=1 and we’ve already sent 2 to 1…)
5 → 1/4
.
.
.
Let's check to be sure that this is a one-to-one correspondence:
Is there a regular pattern here? Yes. There is a logic to this ordering that we can see in the picture; it involves zigzagging back and forth along the diagonal lines. Notice that we can't really see this pattern if we just start listing the actual pairing; it is much, much easier to see the pattern here if we draw the picture. Can this pattern continue forever? Yes. We will be able to continue this zigzagging through the positive rational numbers forever.
If we continue this pattern, will we ever run out of numbers to pair up from each set? No. Since both sets are infinite, we cannot run out of numbers in either set. If we continue this pattern, will we ever skip any numbers in either set? No. Since the ordering which we have established in the positive rational numbers begins at one corner and then zigzags through every diagonal in the set, we will not leave any integers out of the ordering; again, this is really clear when we look at the picture we have drawn, although it is very difficult to see if we just list the order of the numbers. Often, the best way to show a pattern is simply to draw a picture!
So this pairing is a one-to-one correspondence!
Since we have a one-to-one correspondence between the set of positive rational numbers and the set of natural numbers, we can conclude that the cardinality of the set of positive rational numbers is ℵ0!
But what about the set of all rational numbers? Remember that Q is the symbol for the set of rational numbers, and therefore that Q+ is the symbol for the set of positive rational numbers and Q- is the symbol for the set of negative rational numbers. We already know that n(Q+) = ℵ0. And since there must be the same number of negative rational numbers as there are positive rational numbers, we must have n(Q-) = ℵ0 also. Since the set of rational numbers include all the positive rational numbers and all the negative rational numbers, and the number 0 (which is neither positive nor negative), then the total number of elements in the set of rational numbers must be: n(Q) = n(Q+)+n(Q-)+1. So substituting in ℵ0 for n(Q+) and n(Q-) gives n(Q) = ℵ0+ℵ0+1 = 2ℵ0+1. But we know that adding or multiplying ℵ0 by finite numbers like 1 and 2 does not change it! So we can write: n(Q) = 2ℵ0+1 = ℵ0, and therefore we have n(Q) = ℵ0.
So the cardinality of the rational numbers is ℵ0!
What does this tell us about the nature of infinite "numbers"?
It is interesting that ℵ0 describes both the number of natural numbers and the number of rational numbers. This is interesting because the number of rational numbers must be many, many times the number of natural numbers. How many more times? Let's look at our picture of the positive rational numbers again:
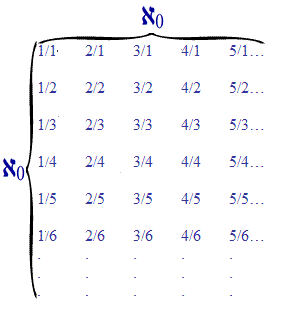
Here we can see that the positive rational numbers make up a kind of square, which has an infinite height and an infinite width. Because each row and each column could be put into one-to-one correspondence with the natural numbers, we can see that the height of this square must be ℵ0 and the width of this square must be ℵ0. Since we know how to take the area of a square - it is just length times height - we know that the number of rational numbers must be ℵ0×ℵ0, which is the same as ℵ02.
So, the cardinality of the set of positive rational numbers must be ℵ02, or in other words, n(Q+)=ℵ02.
But because we can put the set of positive rational numbers into one-to-one correspondence with the set of natural numbers, we know that the cardinality of the set of rational numbers must be ℵ0, or in other words, n(Q+)=ℵ0. So these two quantities must be equal, and this means that ℵ02 = ℵ0!
This may seem like a contradiction at first, because we know that for any finite number n other than 0 or 1, n2≠n. But remember that ℵ0 does not behave like a regular finite number, because it is infinite!
Let's look at this more closely: If we have ℵ02 = ℵ0, then we can multiply both sides of this equation by ℵ0 to get ℵ03 = ℵ02. But since ℵ02 = ℵ0, we can substitute ℵ0 for ℵ02 on the right side of the equation to get ℵ03 = ℵ0.Then if we multiply this equation by ℵ0 on both sides, we get ℵ04 = ℵ02. But since ℵ02 = ℵ0, we can substitute ℵ0 for ℵ02 on the right side of the equation to get ℵ04 = ℵ0.
Notice that we can continue this pattern forever, so we can see that for any regular non-zero finite number n, we have:
ℵ0n = ℵ0
So, raising ℵ0 to the power of any regular finite non-zero number does not change it! (Basically, the idea here is that the infinite "number" ℵ0 is so big, that raising it to any power that is not infinite will not be enough to change it.)
Now let’s take a look at the real numbers:
The set of real numbers is clearly also infinite, but does tit have the same infinite cardinality as the set of natural numbers? It’s difficult to tell.
Remember that the real numbers include any numbers which can be written as a decimal. So to even begin to list them all, we need to list all the possible decimals. Where would we begin? Once we pick a single decimal to start with, what decimal would we choose to come next?
It turns out that the set of real numbers does NOT have the same cardinality as the set of natural numbers, but we need to be able to PROVE that. How do you prove that it is not possible to set up any one-to-one correspondence between a given set and the set of natural numbers? Just showing that one particular correspondence is not a one-to-one correspondence is not enough, because there might be another one-to-one correspondence that works. Instead, we have to come up with a general argument that shows why no pairing between the two sets will be a one-to-one correspondence.
One very common method of PROOF in mathematics is what we call PROOF BY CONTRADICTION. If we want to prove that something is false, we often use this kind of proof. In this method of PROOF, we assume the thing we are trying to prove is false is actually true, and we show that assuming the thing to be true leads to a contradiction . If we assume something is true, and that assumption leads to a contradiction, then we have to conclude that our initial assumption was false. You’ve already seen me use this method of proof. Remember this proof from earlier in the lecture?:
We want to prove that for any finite number n, n ≠ n+1.
We begin by assuming that n = n+1.
Subtracting n from each side gives us 0 = 1.
This is clearly false - it is a contradiction to say that 0=1! So our assumption that n = n+1 which led to this equation must be false.
Therefore we can conclude that for any finite number n, n ≠ n+1.
This proof was a proof by contradiction.
So now let’s try to use proof by contradiction to prove that the cardinality of the set of real numbers is not ℵ0:
We start by assuming the opposite of what we want to prove: we suppose that the cardinality of the real numbers is ℵ0.
This means that the set of real numbers can be put into a one-to-one correspondence with the natural numbers.
Every real number can be written as a decimal, so this means that we can make a list of real numbers written as decimals so that we pair up the first element of the list with the natural number one, the second decimal on the list with the natural number 2 and so on…
For example, our list of real numbers might begin like this:
2.19456283980…
0.73646556586…
0.74654433322…
5.04
3.33333333333...
.
.
.
Now we want to show that there will be a problem lining all the decimals up in this way; the best way to do this is to show that no matter how we line the decimals up, we will always end up leaving a decimal out. Because if we leave a decimal out, then we won't have a one-to-one correspondence.
Let’s try to find a decimal that was left off the list by lining all the numbers up this way:
1 → 20.19456283980…
2 → 0.73646556586…
3 → 0.74654433322…
4 → 5.04
5 → 3.33333333333...
.
.
.
Let’s make a new decimal which is not on the list. For it’s first decimal place, or tenths place, to ensure that this new number is not the same as the first real number on our list, we just need to pick any digit that will be different from the digit in the tenths place of the real number which is paired with the natural number 1. In this case our first number is 20.19456283980…. This number has a 1 in the tenths place. So we just need to pick any digit that is NOT 1 and put it in the tenths place of our new number. Let’s pick 7. So our new number begins 0.7…. Therefore, because they have different tenths digits, this new number cannot be the real number on our list which is paired with the natural number 1.
Now we need to pick this new number’s second decimal place, or hundredths place. To do this in a way that ensures that our new number is not the same number as the second real number on our list, we just need to pick any digit that will be different from the digit in the hundredths place of the real number which is paired with the natural number 2. In this case, the second number on the list is 0.7364655658…. This number has a 3 in the hundredths place, so we just need to pick any digit that is NOT 3 and put it in the hundredths place of our new number. Let’s pick 5. So our new number now begins 0.75…. Therefore, because they have different hundredths digits, this new number cannot be the real number on our list which is paired with the natural number 2.
We repeat this procedure for the third decimal place, or thousandths place, by making sure that the thousandths place of our new number is different from the thousandths place of the third number in our list of real numbers. So in this case we can put any digit except 6 in the thousandths place of our new number, because 6 is the digit in the thousandths place of the third number on the list of real numbers. Let’s pick 1. So now our new number is 0.751…, and is not the third real number on our list.
We repeat this procedure for the fourth decimal place, or ten-thousandths place, by making sure that the ten-thousandths place of our new number is different from the ten-thousandths place of the fourth number in our list of real numbers. So in this case we can put any digit except 0 in the thousandths place of our new number, because 0 is the digit in the ten-thousandths place of the fourth number on the list of real numbers (because 5.04 can be rewritten as 5.0400 without changing it). Let’s pick 1. So now our new number is 0.7511…, and is not the fourth real number on our list.
We keep doing this forever so that, in general, the nth decimal place of our new number is different from the nth decimal place of the nth real number on our list.
If we keep this up, we’ll end up with a new real number written as a decimal that has at least one decimal digit that is completely different from the same decimal place for every single number ion our list of real numbers. Our new number will have a different first decimal place digit than the first number on the list, a different second decimal place digit from the second number on the list, a different third decimal place digit from the third number on the list, a different fourth decimal place digit from the fourth number on the list, etc. Because decimal places go on forever, we will never run out of decimal places so we can be sure that every number on the list of real numbers has at least one decimal place that is different from our new number. So no matter how we line up the real numbers, we can always come up with a new number that is NOT on the list!
But this is a contradiction! If we line up all of the real numbers to make a list, then all of the real numbers are in the list, and we shouldn’t be able to come up with a new real number that is NOT on the list! Because assuming that all the real numbers can be lined up in a particular order leads to a contradiction, we must conclude that our assumption is false, and therefore that the real numbers cannot be lined up in any particular order without leaving some numbers out. Because we can never line up all the real numbers in a particular order, we cannot establish a one-to-one correspondence between the set of real numbers and the set of natural numbers, and therefore the cardinality of the set of real numbers cannot be ℵ0. The cardinality of the set of real numbers must be a different infinite "number!"
So we have found a different infinite “number!” The infinite “number” that describes the number of elements in the set of real numbers is different from ℵ0 because the real numbers cannot be put into a one-to-one correspondence with the natural numbers. We will call this new infinite “number” ℵ1 (or c, which is the symbol which the book uses). So now ℵ1 is an infinite “number,” just like ℵ0, except while ℵ0 describes the number of elements in the set of natural numbers, ℵ1 describes the number of elements in the set of real numbers. Clearly ℵ1 must be a bigger infinity than ℵ0, because the set of real numbers is a bigger set than the set of natural numbers. Just like we say that something is COUNTABLE if it has a cardinality of ℵ0, we say that a set is UNCOUNTABLE if it had cardinality ℵ1. We describe sets with the cardinality ℵ1 as UNCOUNTABLE because they cannot be lined up in order and therefore “counted.” If these sets could be lined up in order and “counted,” we would be able to create a one-to-one correspondence with the integers, and that would mean the set had cardinality ℵ0 instead of ℵ1.
Here's also a way of looking at a picture drawing of ℵ0 compared to ℵ1. Any set which has cardinality ℵ0 is discrete, meaning that it contains distinct, separate elements which can be lined up. For example, if we were to draw the integers on a number line, the picture of that would look like this:
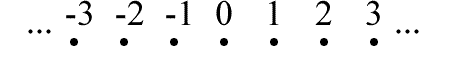
This is a sequence of separate dots. Any set which has cardinality ℵ0 can be drawn in this way, with its elements as a sequence of separate ordered dots.
However, if we were to draw the real numbers on a number line, the picture of that would look like this:
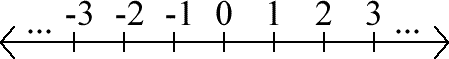
This is a solid, continuous line. Any set which has cardinality ℵ1 can be drawn in this way, with its elements as one continuous line.
This gives us a visual picture of how these infinities are so different from one another. A countable infinity may go on forever in one or more directions, but it does not have an infinite number of elements in between any two elements the way the real numbers do. The elements of a countable set are discrete. However, in an uncountable set, there are so many elements that all the space between any two elements is filled up with an infinite number of other elements, making the set continuous.
So now we have one last infinite set to consider which we have not yet looked at: the set of irrational numbers. (Remember that this is just the set of real numbers that are NOT rational numbers.) Because irrational numbers, like real numbers, can have decimals that go on forever without repeating, we suspect that the irrational numbers have the cardinality ℵ1 of the real numbers instead of the cardinality ℵ0 of the natural numbers. But we need to prove this. Again, we are going to use PROOF BY CONTRADICTION:
First, let’s assume that the irrational numbers have cardinality ℵ0.
If we put together all the rational numbers with all the irrational numbers, we will get the real numbers.
So if we add the cardinality of the rational numbers to the cardinality of the irrational numbers we should get ℵ1.
But if the cardinality of the irrational numbers is ℵ0, this would give us ℵ0+ ℵ0= ℵ1.
But we already know that ℵ0+ ℵ0= 2ℵ0= ℵ0 because multiplying ℵ0 by any finite number does not change it!
So assuming that the rational numbers have cardinality ℵ0, we end up proving that ℵ0= ℵ1, which is a contradiction!
So our assumption that the cardinality of the irrational numbers is ℵ0 must be false.
Therefore the cardinality of the irrational numbers must be ℵ1, the same as the cardinality of the real numbers.
So, finally we have determined the cardinality of all the important infinite sets: (Remember that we write the cardinality of the set A as n(A).)
n(N) = ℵ0
n(Z*) = ℵ0
n(Q) = ℵ0
n(R) = ℵ1 (or c)
n(set of irrational numbers) = ℵ1 (or c)
We can now create a new definition of an infinite set based on what we have learned so far about infinite cardinalities:
If a set can be put into one-to-one correspondence with a PROPER subset of itself, then it is an INFINITE SET.
Clearly, if a set is finite, it cannot be put into one-to-one correspondence with a proper subset of itself because we will run out of numbers in the proper subset to pair up with elements of the set, because a proper subset always has fewer elements than the parent set. But with an infinite set we don’t necessarily have this problem because we never run out of numbers in either set to pair up, each set being infinite.
Be careful not to misread this definition: It says that any infinite set can be put into one-to-one correspondence with A proper subset of itself, but it does NOT say that an infinite set can be put into one-to-one correspondence with EVERY proper subset of itself. For example, the set of real numbers CAN be put into one-to-one correspondence with the set of irrational numbers, which is a proper subset (We know this because we proved earlier that the real numbers and the irrational numbers have the same cardinality ℵ1.). But the set of real numbers CANNOT be put into one-to-one correspondence with the set of rational numbers, as we proved above. Both the set of rational and the set of irrational numbers are proper subsets of the real numbers, but the real numbers can ONLY be put into one-to-one correspondence with the irrational numbers and NOT the rational numbers. Technically, to show that a set is infinite we only have to come up with ONE proper subset of the set that can be put into one-to-one correspondence with the set.
For example, if I want to PROVE that the set of natural numbers is infinite, all I need to do is come up with a subset of the natural numbers that can be put into a specific ordering that goes on forever so that I can set up a one-to-one correspondence. I choose the set of even integers. This set goes on forever because the even integers go on forever, and it is easy to order it. I just set up a correspondence in the following way:
1 → 2
2 → 4
3 → 6
4 → 8
.
.
.
Clearly if I just send each natural number to it’s double, I end up with a one-to-one correspondence. This shows me that the set of even natural numbers can be put into one-to-one correspondence with the natural numbers. The set of even natural numbers is clearly a PROPER subset of the natural numbers because every even natural number is in the set of natural numbers, and the number 1 (or any other odd number in fact) is an element of the natural numbers, but not of the even natural numbers. So by the definition given above, we have proved that the set of natural numbers is an INFINITE SET by showing that it has a proper subgroup with which it can be put into one-to-one correspondence.
Can you find another proper subgroup of the natural numbers that can be put into one-to-one correspondence with the natural numbers?