Lecture 1: Mathematical Review

There are some mathematical concepts that we will use so often in this class that it is important that we take the time to review them now, before we begin any new material. Each of the mathematical ideas explained below should be something that you've done before in a class that is a prerequisite to this one; however, we are covering them briefly here because you will be unable to do any of the problems in this class if you do not remember these important mathematical techniques from previous classes.

Relative Value, Addition, Subtraction and Multiplication of Decimals

We need to be able to compare the sizes of decimals and to add, subtract, multiply and divide them.

Comparing the sizes of 2 or more decimals:

To begin our discussion of decimals, we must first review the place value of each number in a decimal. Remember that the first number after a decimal is always the tenths place, the second number after the decimal is always the hundreds place, the third number after the decimal is always the thousands place, and so on. Likewise, the first number to the left off the decimal is the ones place, the number to the left of the ones place is the tens place, the number to the left of the tens place is the hundreds place, and so on:

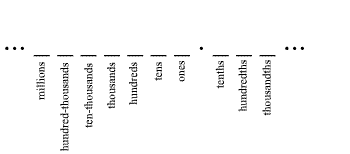
So, for example, the number 504.205 has 5 hundreds, 4 ones, 2 tenths, and 5 thousandths. To compare the relative sizes of two decimals, we will need be able to identify each place value in the decimal. To see which decimal is bigger, we go from left to right; we begin by looking at the place value farthest to the left and comparing its digit in each number. If the place value farthest to the left is the same in each number, then we look at the next place value to the right, and if that digit is the same in each number, we keep going to the next place value to the right until we find a digit that is different in each number. (If all the digits are the same in every place value, then the two numbers we are comparing must be exactly the same!)

Example:
Let's compare 2.45 and 5.4. We begin by looking at the place value the farthest to the left. In this case that is the ones place. The ones place in 2.45 is 2, while the ones place in 5.4 is 5. Because 2<5, we know that 2.45<5.4.
Example:
Let's compare 0.34 and 0.304. We begin by looking at the place value the farthest to the left. In this case that is the tenths place. The tenths place is 3 in 0.34 and 3 in 0.304. Because the tenths place is the same in both numbers, we have to look at the next digit to the right, which is the hundredths place. The hundredths place is 4 in 0.34 and 0 in 0.304. So because 4>0, we can conclude that 0.34>0.304.
Example:
Let's compare 0.026 and 0.26. We begin by looking at the place value the farthest to the left. In this case, the hundredths place is the place value the farthest to the left in 0.026, and the tenths place is the place value the farthest to the left in 0.26. Because the hundredths place represents
1
100
and the tenths place represents
1
10
and
1
100
<
1
10
, we know that 0.026<0.26.
Now it's time for you to practice some problems of your own.

Rounding Decimals

To round a decimal to a particular decimal place, we must first look at the number exactly to the right of the place where we want to round off:
  1. If the number to the right of the place where we want to round is less than 5, then we round down. This means that we leave the number in the place where we want to round the same; then we leave off any numbers in decimal places to the right of this spot.
  2. If the number to the right of the place where we want to round is greater than or equal to 5, then we round up. This means that we take the number in the place where we want to round and increase it by one; then we leave off any numbers in decimal places to the right of this spot.

Sometimes when the number we are trying to round up is a 9, we actually have to round the 9 up to a 0, and then increase the number directly to the left of it by one; this is like rounding the 9 up to a 10 - we just can't put the number 10 in a single place - we can only write it by going up by one, one place value to the left.

Example:

Round 3.45 to the nearest tenth.

We want this number to stop at the tenths place, so we look at the number just to the right of the tenths place, the number in the hundredths place:

3.45                                                                                                                                                                                                                                                                                                                                          3.45

Because the number in the hundredths place is 5, we round up, so we change the 4 in the tenths place to a 5 and leave all numbers that come after the 4 off when we right the rounded number:

3.5

Example:

Round 3.452 to the nearest hundredth.

We want this number to stop at the hundredths place, so we look at the number just to the right of the tenths place, the number in the thousandths place:

3.452

Because the number in the thousandths place is 2, we round down , so we leave the 5 in the hundredths as a 5 and leave all numbers that come after the 5 off when we write the rounded number:

3.45

Example:

Round 1.99 to the nearest tenth.

We want this number to stop at the tenths place, so we look at the number just to the right of the tenths place, the number in the hundredths place:

1.99                                                                                                                                                                                                                                                                                                                                          3.45

Because the number in the hundredths place is 9, we round up, so we change the 9 in the tenths place to a 0, and change the number 1, which is one place to the left of the tenths place, to a 2; then we leave all numbers that come after the tenths place off when we write the rounded number:

2.0=2

In this course we will always want to eliminate extra zeros after the decimal point because when working with drug dosages, misreading the number or the units of the dosage is one of the most common reasons for patients being dosed incorrectly. Because 2.0 may sometimes be misread as 20, even though it is the more "mathematically correct" way of writing the answer, we will always write 2.0 as 2 instead, because we are more interested in making sure that the dosage will not be misread.

Adding Decimals

To add two decimals, we:
  1. Line up the decimal points.
  2. Add as usual, keeping the decimal point of the answer lined up with the decimal points of the numbers we are adding.
Note: If there is no decimal point in a number, we can always put one in it after the ones place and then put zeros after it without changing the value of the number.
Example:

34.5+7

First we line up the decimal points:

34.5
+7    

Then we add and carry as needed:

1
34.5
+7    
41.5
Example:

2.96+19.3

First we line up the decimal points:

     2.96
+19.3    

Then we add and carry as needed:

  1 1
     2.96
+19.3    
  22.26

Subtracting Decimals

To subtract two decimals, we:
  1. Line up the decimal points.
  2. Add zeros after the decimal point to the first number in the subtraction problem; you will need the first number to have at least the same number of digits after the decimal point as the second number so that you can subtract!
  3. Subtract as usual, keeping the decimal point of the answer lined up with the decimal points of the numbers we are adding.
Note: If there is no decimal point in a number, we can always put one in it after the ones place.
Also, be careful while borrowing!
Example:

34.5−7

First we line up the decimal points:

34.5
−7    

Then we subtract and borrow as needed:

214
34.5
−7    
27.5
Example:

20−9.99

First we line up the decimal points:

    20
−  9.99   

Then we put the decimal point and 2 zeros after 20 because we recall that 20=20.00:

   20.00
−   9.99   

And finally we subtract and borrow as needed:

   110
   20.00          We need to borrow to subtract 9 from 0, so we keep going to the left until we can borrow -
−   9.99               we borrow from the 2.

      9
   11010
   20.00          Now we keep borrowing until we can subtract the 9 from the 0 on the far right-
−   9.99               we borrow from the 10.

      9   9
   1101010
   20.00          Now we keep borrowing until we can subtract the 9 from the 0 on the far right-
−   9.99               we need to borrow from the second 10, and then we can subtract.
   10.01

Multiplying Decimals

To multiply two decimals, we:
  1. Multiply as usual, ignoring the decimal points for the moment. Be sure to leave any zeros at the end!
  2. Count the number of digits after the decimal point in the two numbers you are multiplying.
  3. Take the number you got in step 2 and move the decimal place that many places from the right in your answer. Zeros count as a place when you are moving the decimal in this step!
Example:

34.5×7

First we multiply, ignoring the decimal points:

    33
  34.5
×   7  
2415

Then we count the number of digits after the decimal place in the numbers we are multiplying - in this case there is only 1 digit total (one in 34.5 and none in 7):

        33
  34.5
×   7  
2415

So now we count 1 digit from the right in our answer, and we put the decimal place there:

241.5
Example:

6.25×32.4

First we multiply, ignoring the decimal points:

                      1
           1
        1 2
        6.25
    ×32.4  
       2500
     1250
+1875        
  202500

Then we count the number of digits after the decimal place in the numbers we are multiplying - in this case there are 3 digits total (two in 6.25 and one in 32.4):

                6.25
    ×32.4  
  202500

So now we count 3 digits from the right in our answer, and we put the decimal place there:

202.500

Notice that we can eliminate any unnecessary zeros after the decimal point at the end, so this becomes:

202.5

Dividing Decimals

To divide one decimal by another, we:
  1. Turn both decimals into whole numbers by multiplying each one by a power of 10. As long as you multiply both numbers by the same power of ten, you will not change the answer to the division problem.
  2. Make sure to put the correct number under the long division sign. The first number is the number that is getting divided up and the second number is the number that is doing the dividing.
  3. Put a decimal point above the decimal point in the number below the division bar.
  4. Divide as usual - if you need to, you can add as many zeros as you like after the decimal point to the number below the fraction bar.
  5. Keep dividing until you get a zero remainder, or until you have one digit beyond the place you need to round to. (For example, if you are rounding to the tenths place, you cannot stop dividing after you have the tenths place because you will not know whether you should round up or down - to round to the tenths place you must keep dividing until you have the hundredths place. )
Example:

34.5
7
(Round your answer to the nearest hundredth.)

 

First we multiply by a power of 10 to turn both numbers into whole numbers. Because 34.5 is the only decimal here and we only need to move the decimal place over one spot to make it a whole number, we multiply both numbers by 10:

34.5×10
7×10
=
345
70

Now we set up our long division. Because 345 is on the top, it is what is being divided up, so it goes under the division sign, and because 70 is on the bottom, it is what is doing the dividing, so it goes to the left of the division sign:

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                
70|345

So now we add zeros after the decimal point in 345; since 345 is a whole number, we have to write in the decimal point after the 5, and then we can add as many zeros at the end as we like. We also write in a decimal point above the decimal point in 345:

          

            .
70|345.000

So now we divide as usual. We must keep going until we get to the thousandths place because we need to round to the hundredths place :

          

          4.928
70|345.000
   −280 ↓ ↓ ↓
        650 ↓ ↓
      −630 ↓ ↓
           200 ↓
         −140 ↓
              600

          

So now we round 4.928 to the hundredths place; since 8 is the number in the thousandths place and it is greater than or equal to 5, we can then round it to:

          

4.93

Example:

6.25
32.4
(Round your answer to the nearest hundredth.)

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                     

First we multiply by a power of 10 to turn both numbers into whole numbers. Because 6.25 has two numbers after the decimal place (and 32.4 has only one number after the decimal place, we multiply both numbers by 100:

6.25×100
32.4×100
=
625
3240

Now we set up our long division. Because 625 is on the top, it is what is being divided up, so it goes under the division sign, and because 3240 is on the bottom, it is what is doing the dividing, so it goes to the left of the division sign:

3240|625

So now we add zeros after the decimal point in 625; since 625 is a whole number, we have to write in the decimal point after the 5, and then we can add as many zeros at the end as we like. We also write in a decimal point above the decimal point in 625:

                 .
3240|625.000

So now we divide as usual. We must keep going until we get to the thousandths place because we need to round to the hundredths place :

          

               0.192
3240|625.000
        −3240 ↓ ↓
           30100 ↓
         −29160 ↓
                9400 

So now we round 0.192 to the hundredths place; since 2 is the number in the thousandths place and it is less than 5, we can then round it to:

          

0.19

Decimal Word Problems

Because this class is specifically concerned with calculating dosages, we will always be doing word problems. So in order to sucessful in setting up our word problems, we need to practice.

The math operations we use in this class are very simple: addition, subtraction, multiplication, or division. So all we need to do is to try to determine when to do each of these operations. Let's remind ourselves what each of these operations are for:

  1. A problem that talks about finding the total of something, or describes combining or putting things together is telling us to add, because addition is the process of putting things together.
  2. A problem that talks about finding the difference between two amounts, or finding out what is left after something is taken away is telling us to subtract, because subtraction is the process of taking one thing from another, or finding the difference between two things.
  3. A problem that talks about doing something multiple times, especially when putting things together to find a total is telling us to multiply, because multiplication is the process of adding or combining things multiple times.
  4. A problem that talks about breaking a total or a whole down into smaller pieces is asking us to divide, because division is the process of taking a whole and breaking it into several equal pieces.
So to get a better idea about how to do these word problems, let's look at a few examples:
Example:

This morning you gave a patient 3.5 mg of a drug, and then this afternoon you gave them 4 mg; how much of the drug has the patient taken today?

Notice that this question is asking for the total amount of the drug the patient has taken after a few dosings - this clearly points to addition, so the problem is written:

3.5 mg +4 mg

This equals:

7.5 mg

Example:

You need to give a patient a dosage of 2.8 mg, but you only have one tablet labeled 0.7 mg. How many more milligrams do you need to give the patient this dosage?

Notice that in this question, they are looking for how many milligrams we have left to find after we take into account the part of the total dosage that can be made up by the 0.7 mg tablet. So we are taking 0.7 mg away from the total 2.8 mg to see what is left. This process indicates subtraction, so the problem is written:

2.8 mg − 0.7 mg

This equals:

2.1 mg

Example:

Prepare a dosage of 3.2 mg using tablets with a strength of 1.6 mg. How many tablets do you need to give this dosage?

In this problem, you are asked to take a total amount, 3.2 mg, and break it down into equal pieces - separate tablets, each with a strength of 1.6 mg. This process of taking a whole or a total and finding the number of pieces it will break down into is division, so the problem should read:

3.2 mg
1.6 mg

Which equals:

2 tablets

Example:

The tablets available are labeled 10.5 mg and you are to give 3

1
2
(3.5) tablets. What total dosage will this be?

Here you are finding a total dosage, so your first instinct might be to add, which you could do if you added each tablet separately: 10.5 mg + 10.5 mg + 10.5 mg + 5.25 mg

However, since we are giving the same amount (the 10.5 mg that is in each tablet) multiple times, it makes sense to multiply, so that the problem looks like this:

10.5 mg × 3.5 mg

This equals:

36.75 mg

Simplifying Products of Fractions

Often when we are multiplying several fractions together, it is easier to simplify them first, before we multiply them. Remember that to multiply fractions, we multiply straight across the top and straight across the bottom.
  1. To multiply fractions, multiply straight across the top and straight across the bottom.
  2. If you have any decimals in your fraction, you can get rid of them by multiplying both the top and the bottom of the fraction by a power of 10.
  3. We can only cancel, or divide by a number, if we cancel it out once on the top and once on the bottom .
  4. Keep cancelling until you cannot cancel anything else. You will often have to cancel more than once!
Example:

1.3
0.75
×
0.9
1

First we get rid of the decimals. In this case, we want to turn 0.75 in the bottom into 75. We can do this by multiplying by 100, but if we multiply the bottom by 100, we must also multiply the top by 100:

1.3×100
0.75×100
×
0.9
1
=
130
75
×
0.9
1

Now we need to get rid of the decimal 0.9, so we want to turn 0.9 in the top into 9. We can do this by multiplying by 10, but if we multiply the top by 10, we must also multiply the bottom by 10:

130
75
×
0.9×10
1×10
=
130
75
×
9
10

Now we can work on simplifying the numbers 130, 75, 9 and 10 in the fractions by multiplying straight across to get one big fraction:

130×9
75×10

Now we can "cancel" things out in the top and the bottom by dividing numbers in the numerator and the denominator of the fraction by the same number. In this problem, we can divide both 130 and 10 by 10, and we can divide both 9 and 75 by 3:

130×93
2575×10
=
13×3
25×1
=
13×3
25

Now we should continue to cancel until we cannot cancel anymore, but we notice that we cannot cancel anymore because the only number that goes into 25 is 5, but 5 does not go into 13 or 3.

So, since we cannot cancel anymore, we will multiply across the top and the bottom:

13×3
25
=
39
25

Now all that is left for us to do is to divide 39 by 25, and then round off our answer. Here we will round to the nearest tenth. (In any assignments you receive in this class, the instructions will always tell you what place to round to, if you do not get an exact answer.):

39÷25=1.56

So now we round 1.56 to the nearest tenth to get:

1.6

Example:

44
1
×
1
2.2
×
2.1
1

First we get rid of the decimals. In this case, we want to turn 2.1 in the top into 21. We can do this by multiplying by 10, but if we multiply the top by 10, we must also multiply the bottom by 10:

44
1
×
1
2.2
×
2.1×10
1×10
=
44
1
×
1
2.2
×
21
10

Now we want to turn 2.2 in the bottom into 22. We can do this by multiplying by 10, but if we multiply the bottom by 10, we must also multiply the top by 10:

44
1
×
1×10
2.2×10
×
21
10
=
44
1
×
10
22
×
21
10

Now we can work on simplifying the numbers in the fractions by multiplying straight across to get one big fraction:

44×10×21
1×22×10

Now we can "cancel" things out in the top and the bottom by dividing numbers in the numerator and the denominator of the fraction by the same number. In this problem, we can divide both 10 and 10 by 10, and we can divide both 44 and 22 by 22:

442×10×21
1×122×10
=
2×1×21
1×1×1
=
2×21
1
=2×21

Now we should continue to cancel until we cannot cancel anymore, but we notice that we cannot cancel anymore because there is nothing left in the bottom except 1.

So, since we cannot cancel anymore, we will multiply across the top and the bottom:

2×21=42

Example:

7.5
12.3
×
55
5
×
23.2
1.2

First we get rid of the decimals. In this case, we want to turn 7.5, 12.3, 23.2, and 1.2 into whole numbers; because each of this will be a whole number if we multiply them by 10, we take both the first and the last fraction above and multiply both the top and the bottom of each fraction by 10:

7.5×10
12.3×10
×
55
5
×
23.2×10
1.2×10
=
75
123
×
55
5
×
232
12

Now we can work on simplifying the numbers in the fractions by multiplying straight across to get one big fraction:

74×55×232
123×5×12

Now we can "cancel" things out in the top and the bottom by dividing numbers in the numerator and the denominator of the fraction by the same number. In this problem, we can divide both 75 and 3 by 3, and we can divide both 232 and 12 by 34:

75×5511×23258
123×15×312
=
75×11×58
123×1×3

Now we can reduce this fraction even further, by dividing 75 and 3 by 3:

7525×11×58
123×1×13
=
25×11×58
123×1×1
=
25×11×58
123

Now we should continue to cancel until we cannot cancel anymore, but we notice that we cannot cancel anymore because the only number that goes into 25 is 5, but 5 does not go into 123; likewise, 11 does not go into 123, and 2 and 29 are the only two numbers which go into 58, but neither of these two numbers goes into 58.

So, since we cannot cancel anymore, we will multiply across the top and the bottom:

25×11×58
123
=
15950
123

Now all that is left for us to do is to divide 15,950 by 123, and then round off our answer. Here we will round to the nearest whole number. (In any assignments you receive in this class, the instructions will always tell you what place to round to, if you do not get an exact answer.):

15,950÷123=129.6... (this decimal keeps going on forever, but we can stop dividing once we know what number is in the tenths place, because we will round to the ones place)

So now we round 129.6 to the nearest whole number to get:

130